反常积分判敛方法

首先通过瑕点把反常积分分成两个积分（只有一个瑕点的就不用了），瑕点就是使分母为0的无意义点或者分母趋于无穷的点。然后分别判敛，下面通过一个例题梳理一下过程：

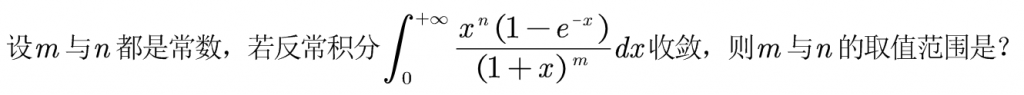
首先来看有几个瑕点，乍一看就一个当x趋于无穷大时，分母趋于无穷大，实则有两个，因为x的n次方，n可能取负，这样当x=0时，分母就等于0了。

接下来拆分：

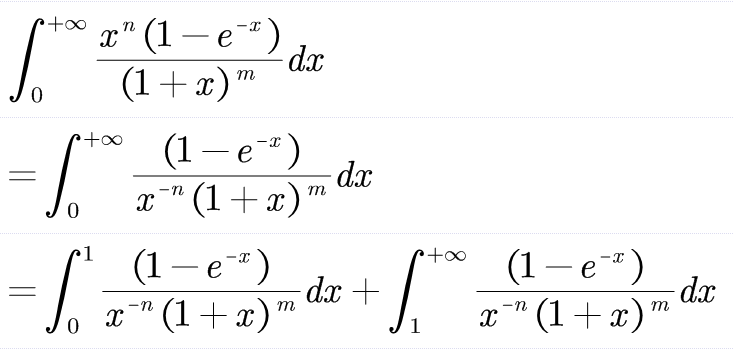
为什么选择从1这点拆开呢，实际上没有要求，2，3，都可以，只要把零和正无穷分开就行，接下来逐个来看：

整理完毕开始判断敛散性（或者已知敛散性求参数）

继续分析另一个积分：

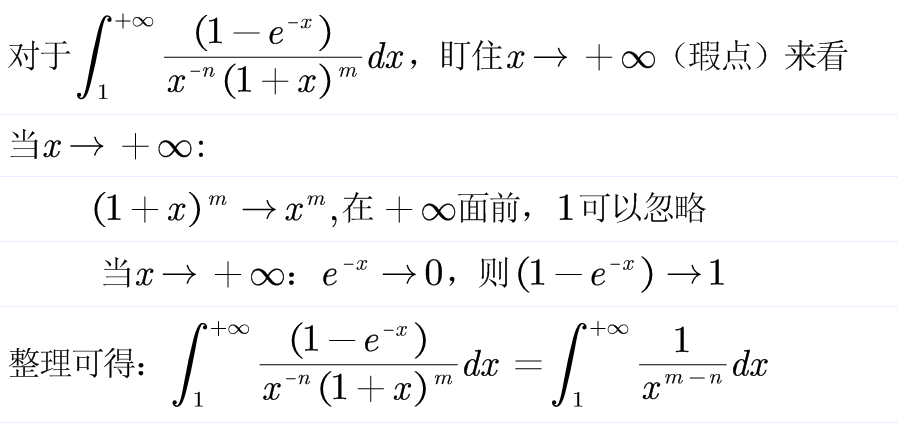
整理完毕开始判敛（依然根据P级数判敛法）

所以根据以上分析，若要满足原始反常积分收敛，则m,n需满足以下条件：

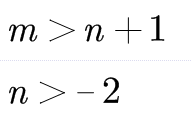
下面补充P级数判敛知识点：