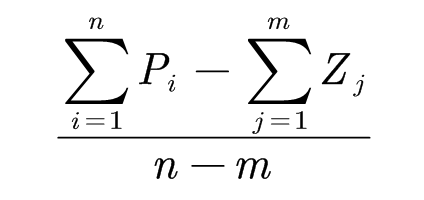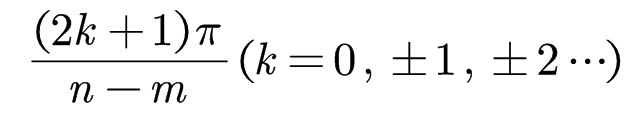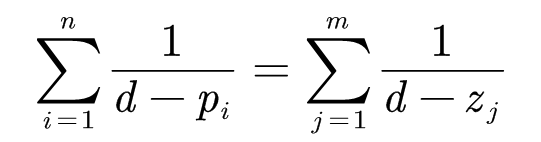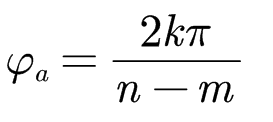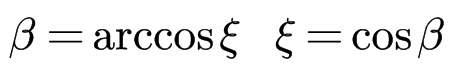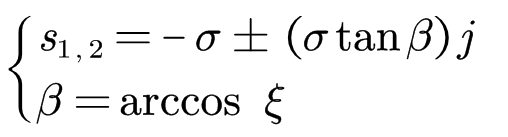闭环根轨迹专题

在一个连续线性定常控制系统中，通常可以根据其闭环传递函数的闭环极点是否全部处于S平面的左半平面，来判断系统的稳定性，如果系统稳定，则所有的闭环极点全部具有负实部（位于S平面左半平面）。根轨迹的绘制，其本质就是根据开环传递函数的极点和零点，去判断闭环极点的位置（随开环根轨迹增益或其他参数的变化，闭环极点在S平面上的轨迹），以此可以判断系统的闭环稳定性和稳定程度。

根轨迹根据特征方程的不同，分为零度根轨迹和180度根轨迹，绘制略有区别，一一介绍。

一、180度根轨迹

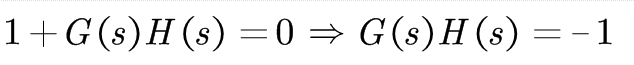
开环传递函数=-1，-1与实轴正半轴夹角180度故称180度根轨迹。

规则1：实轴上根轨迹：从右往左数，奇数个零极点的左侧一段是根轨迹

规则2：渐近线规则：渐近线与实轴交点坐标公式如下:

简单描述就是：所有极点之和减去所有零点之和，除以极点个数减去零点个数

渐近线与实轴正半轴夹角公式如下：

规则3：分离点规则：

注意：如果没有零点，则右侧直接等于0

规则4：起始角（复数极点，起点处切线，与正实轴夹角）规则：

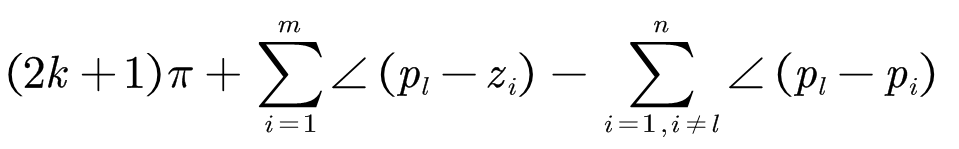
公式看起来比较复杂，实际操作起来较为简单，拆解解释一下：

终止角与之相对应公式如下：

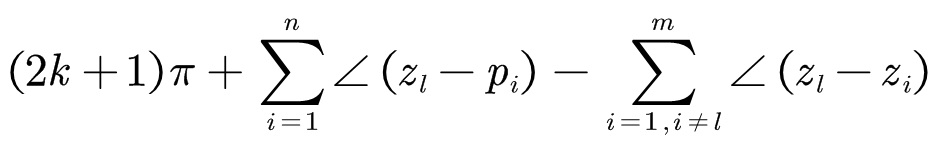
规则5：根轨迹与虚轴交点

补充其他规则：

根轨迹分支数等于闭环特征方程阶数，开环极点个数n

根轨迹关于实轴对称

根轨迹始于开环极点，止于开环零点（m条）或无穷远（n-m条）

二、0度根轨迹

与180度根轨迹相比，0度根轨迹的绘制法则只有和相角有关的规则略有不同，一般是正反馈或者系统增益为负时画0度根轨迹。

实轴上根轨迹不同：从右往左偶数个零极点之左，第一个零极点之右

渐近线与实轴夹角不同：

起始角终止角不同：

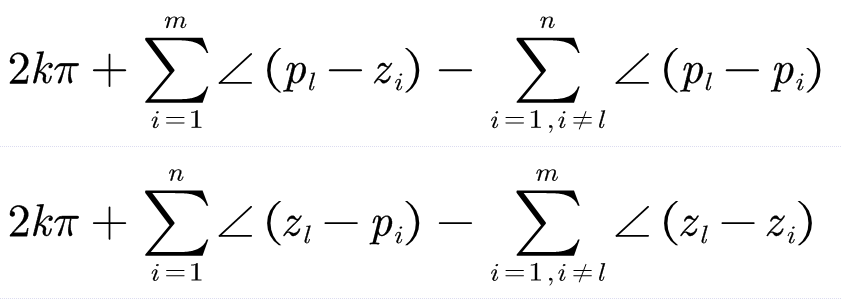
三、根轨迹补充知识

闭环根轨迹能够体现一个控制系统的所有特性

1.当闭环根轨迹穿越虚轴到达S平面右半平面，此时系统不稳定，由此可以求出临界稳定时的增益K和纯虚根。

2.闭环根轨迹上的点与原点连线，连线与负实轴的夹角β，能够体现此时系统的阻尼比，超调量

3.由2.我们就可以设出固定阻尼比时的复数根，带入特征方程，待定系数求出具体根的数值，进而可以求出其他的闭环根

四、来个例题

第一问就是常规的广义根轨迹，第二问比较有意思。

至此这道题目完美解决。

注意：求出闭环极点（与开环零极点和根轨迹增益有关），闭环系统零点由前向通道零点和反馈通道极点组成 ，对于单位反馈，闭环零点就是开环零点