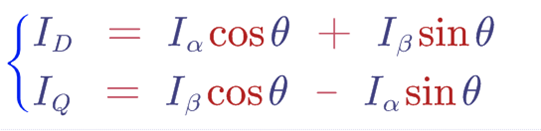FOC学习笔记（三）—-坐标变换之Park变换

一、理论分析：

与Clark变换不同的是，Park变换不是三相到两相的变换，而是静止两相坐标系到旋转两相坐标系的变换，在上一节的Clark变换中，我们得到的变换结果是两相正弦信号。正弦信号对于我们控制来说，比如PID跟踪仍然是困难的，Park变换就是解决这个问题，Park变换之后的坐标系是d-q坐标系，与α-β坐标系不同的是，d-q坐标系是跟随转子旋转的坐标i，这样就相当于把正弦信号的变换转移到坐标系本身了，所以在d-q坐标系下我们应该看到两个恒定的信号，把正弦信号拉直了。

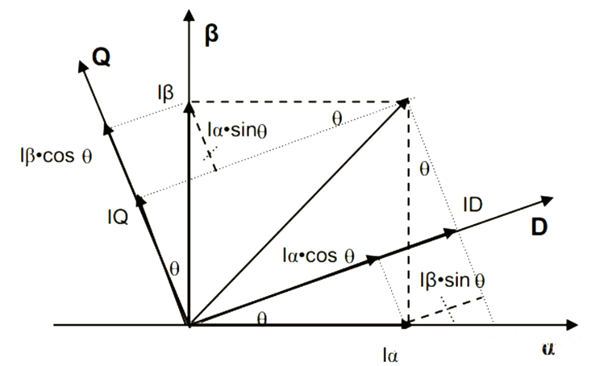
如上图所示，d-q坐标系与α-β坐标系直接夹角θ，此θ是随转子转动的，应该注意的是，Park变换和后面讲的反Park变换中所需要传入的角度θ都是电角度而非转子的机械角度。接下来开始进行数学的分析：

我们把α和β轴上的 I_α ，I_β通过正交分解，分解到d-q坐标轴上去，I_α在d轴上的分量 = I_αcosθ，I_β在d轴上的分量 = I_βsinθ，I_α在q轴上的分量 = -I_αsinθ，I_β在d轴上的分量 = I_βcosθ，综上可以得到如下结果：

二、Matlab仿真

这就是Park变换的数学模型了，接下来通过Matlab仿真查看一下变换结果：

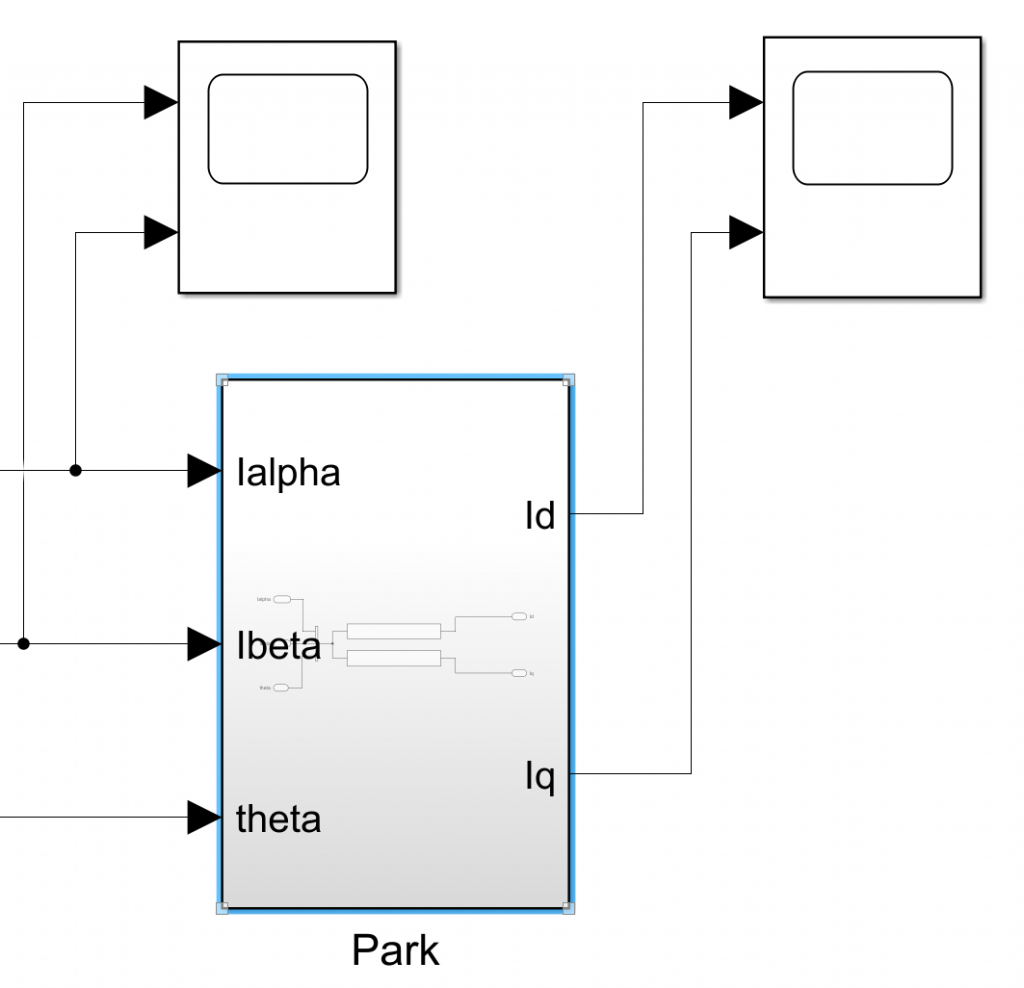
创建Park变换的子系统

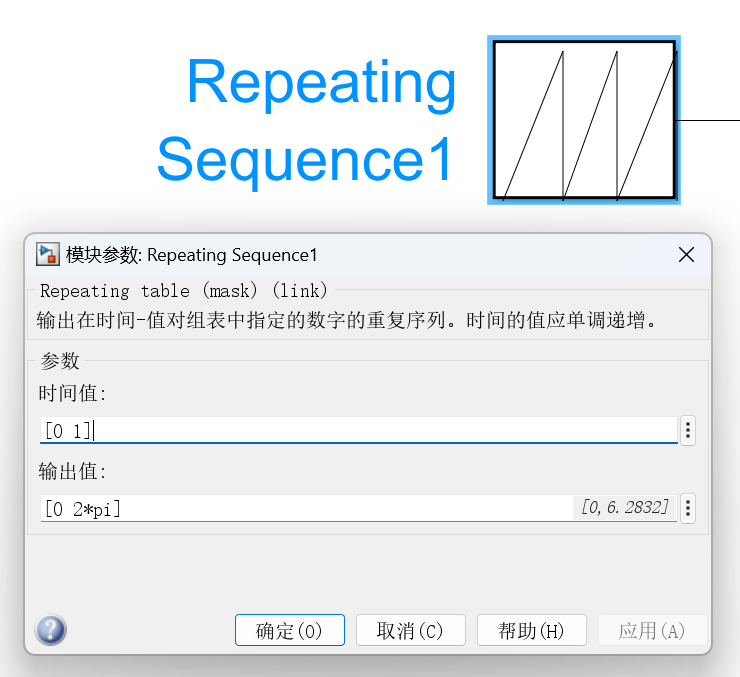
把经过Clarka变换后得到的Iα，Iβ输入到Park变换模块，除此之外还需要一个theta信息，这里使用Repeating Squence模块模拟了一个Theta角度信息0-2pi，

查看变换前后仿真波形：

仿真结果和理论预期一致，Park变换之后得到两个常量。

仿真结果符合理论预期之后，接下来开始在单片机上进行实现。

三、MCU软件实现：

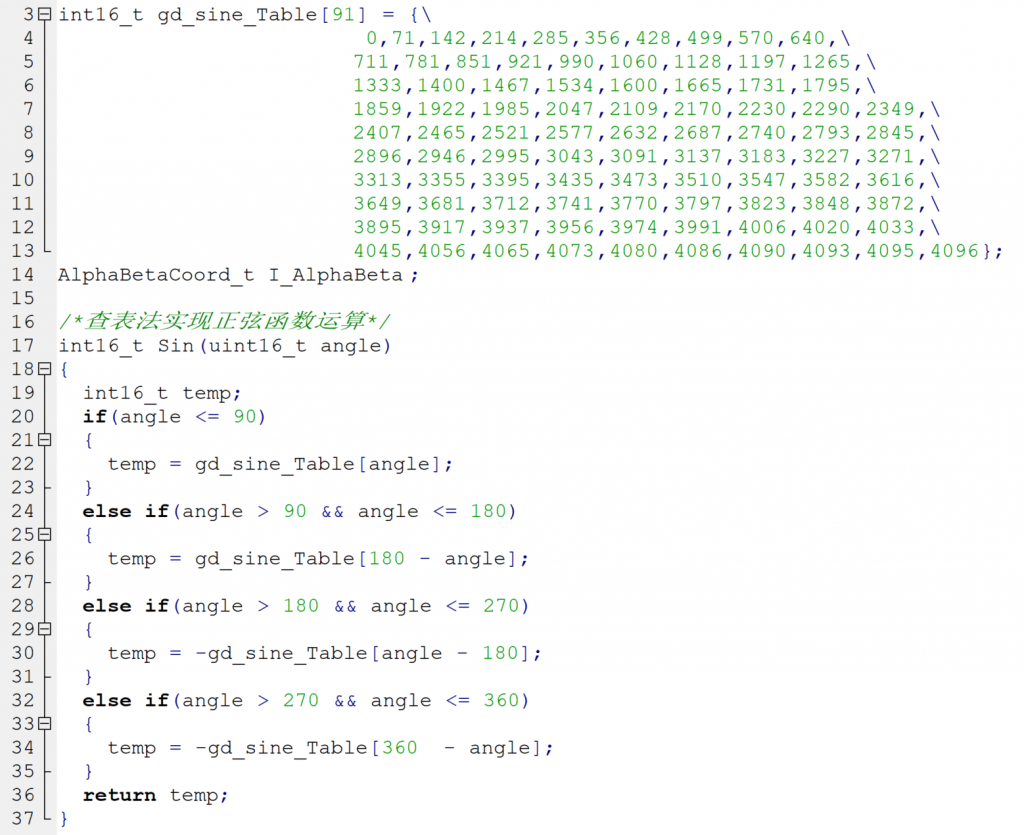
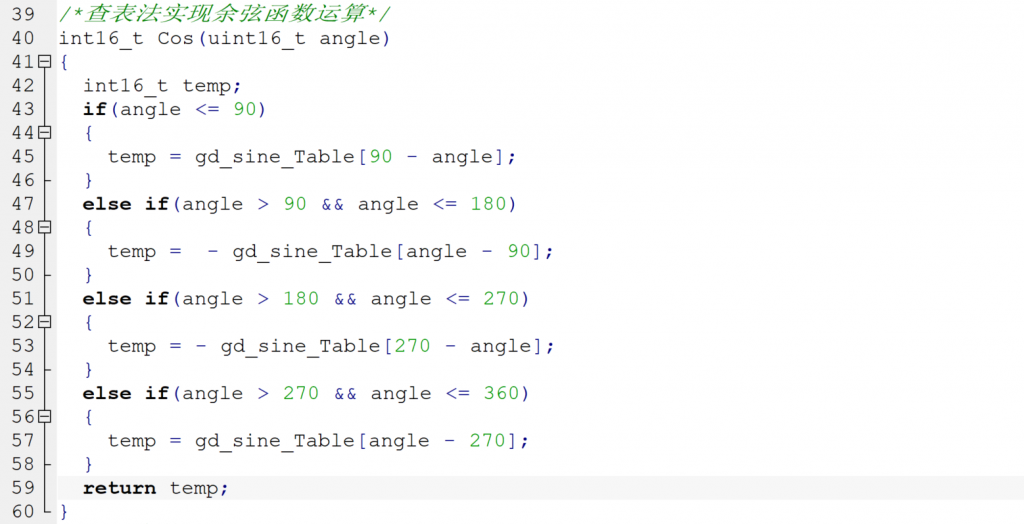
其中Sin和Cos函数实现如下：

其中的结构体定义如下：

调用Park变换函数，打印计算结果通过上位机绘制数据变换波形，可见MCU计算 波形和仿真波形一致：

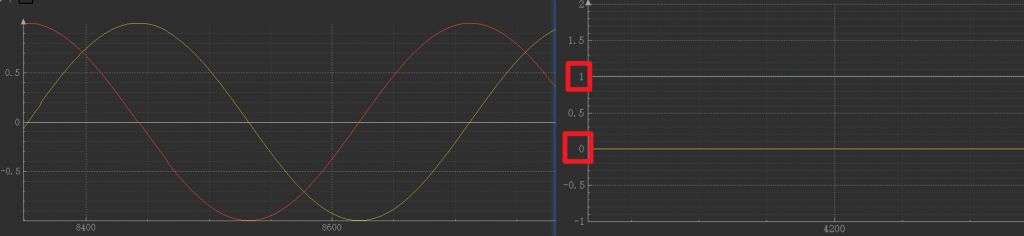
Park变换至此结束。