FOC学习笔记(二)—-坐标变换之Clark变换
简而言之,Clark变换就是三相到两相的便变换,过程如下:
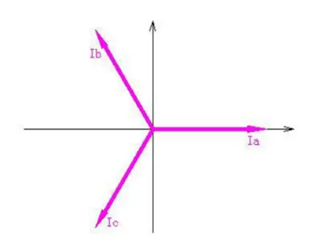
如图,粉红色部分就是三相坐标系下的Ia,Ib,Ic,两两互差120°,黑色部分是α-β坐标系,是一个正交坐标系,两者互差90度。
首先提到一个概念,等幅值变换和等功率变换,等幅值变换是指变换前后分量幅值相等,如上图可以理解为,Ia和Iα大小完全重合。这种情况下变换过程需要乘以一个系数,这种变换更加清爽符合我们的直觉,所以网络上的的大部分文章都是基于等幅值变换。等功率变换就不能保证Iα和Ia重合,其实无论是等幅值变换还是等功率变换都无所谓,因为电机不在乎幅值是否相等,功率是否相等,电机在乎的是磁通矢量是不是相等,无论哪种变换,磁通矢量都是相等的,这其中涉及到一个等效匝数比的概念,3相变两2相这其中的等效匝数比就是2/3,这也是等幅值变换中那个系数的来源。
类似于正交分解,我们把Ia,Ib,Ic向α-β坐标轴上做投影然后合并,得到如下公式:
使用矩阵形式表达如下:
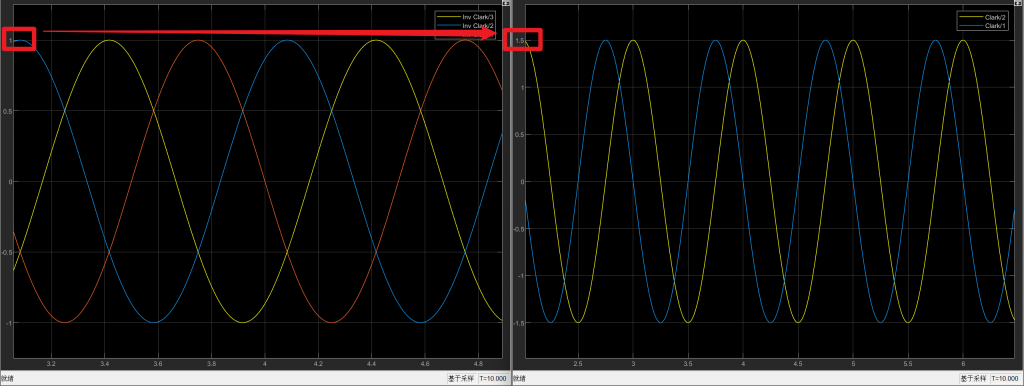
再此变换下,通过仿真我们不难看出,变换后的幅值变成了1.5,这就是我们所说的等功率变换,就不能保证变换前后的分量幅值相等。
所以我们手动乘以2/3,以保证变换前后分量幅值相等。
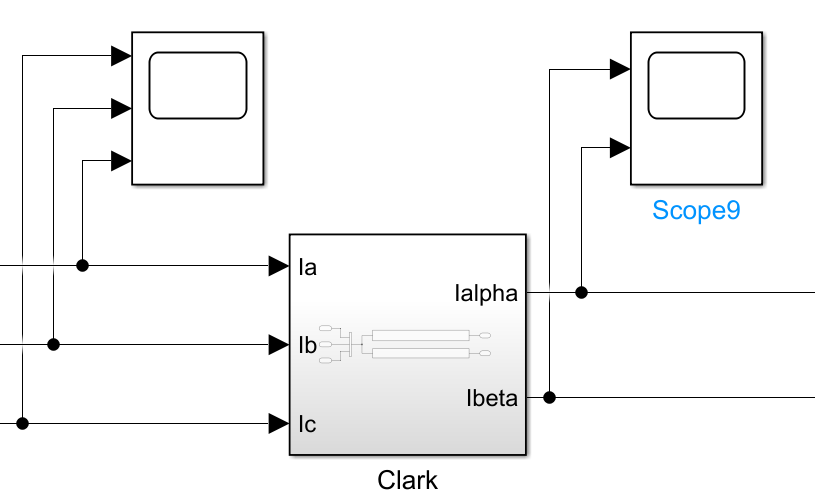
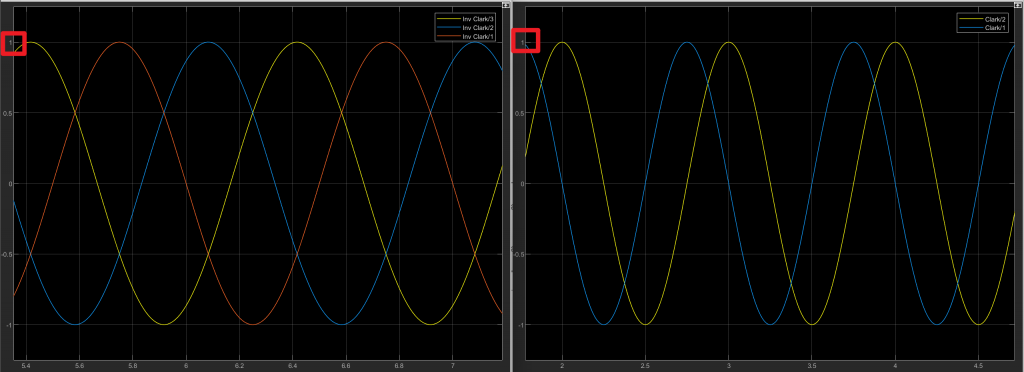
这就是等幅值Clark变换的变换矩阵。通过仿真可以看到变换前后的结果:
可以看到变换前后,幅值相等,少了一个分量,接下来开始在硬件平台上实现:
至于这里/6144是什么意思,这涉及到我这里Sin()和Cos()是查表法实现的,减少MCU的运算压力,查表放大了4096倍,及sin的0-1在我这里是0-4096用来保留一定的精度,原本是/4096恢复浮点值,然后结合Clark变换前面我们讲到的等幅值变换中的2/3,结合计算一下就是/6144保证变换前后分量幅值相等。
然后我调用此函数,打印输出结果:
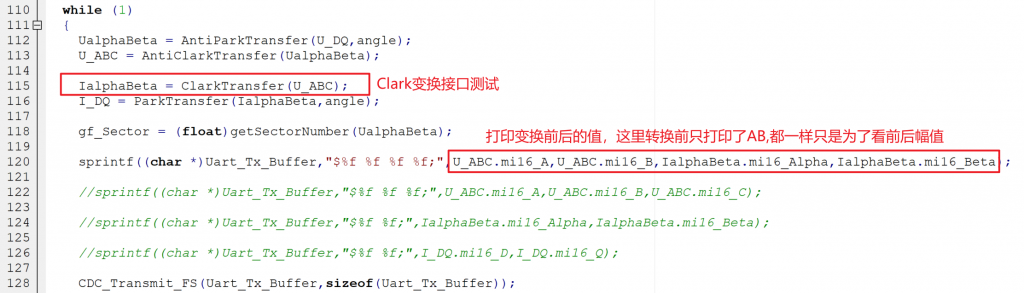
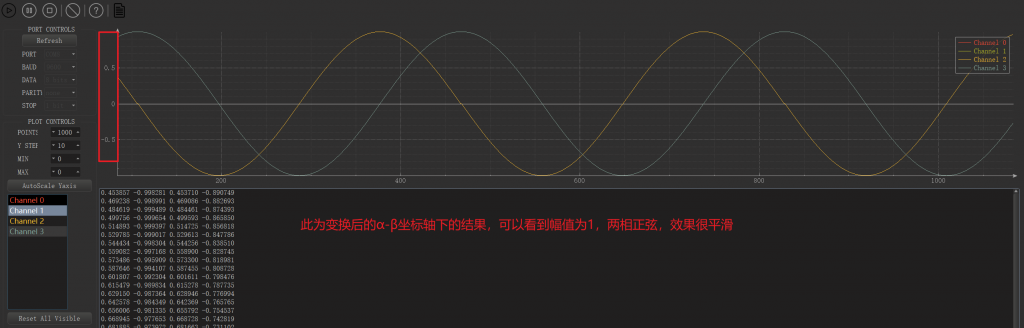
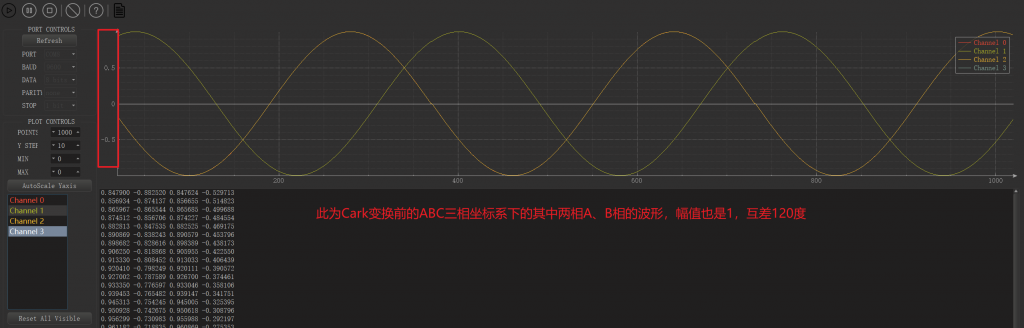
通过上位机查看波形:
可以看到,硬件平台的实现效果和Matlab仿真效果完全一致,Clark变换至此结束。


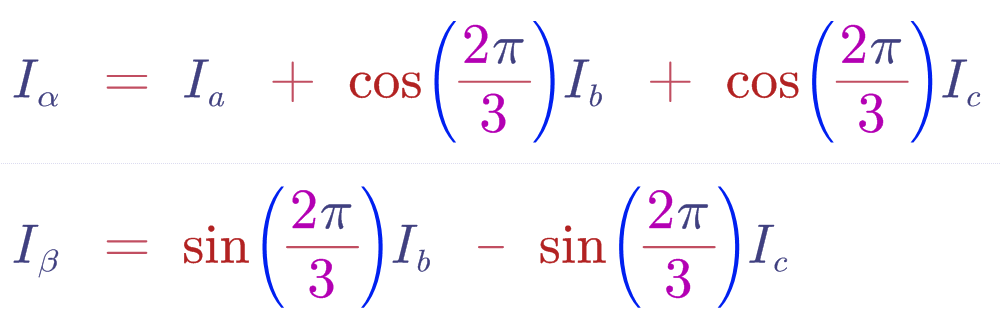
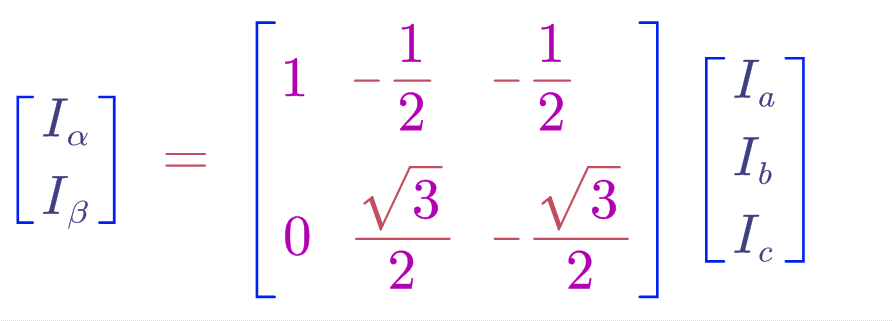
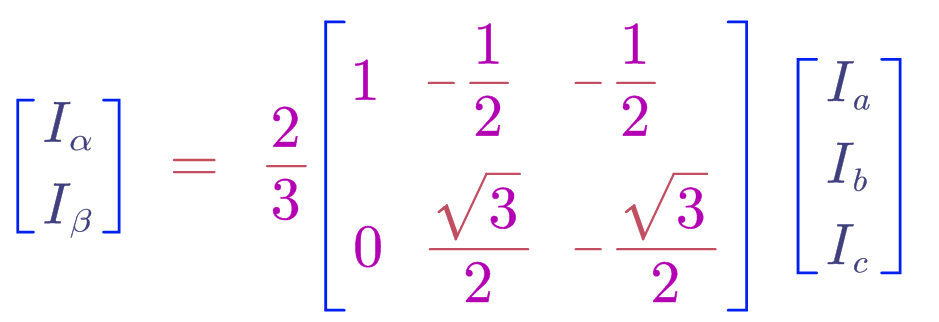

1 thought on “FOC学习笔记(二)—-坐标变换之Clark变换”