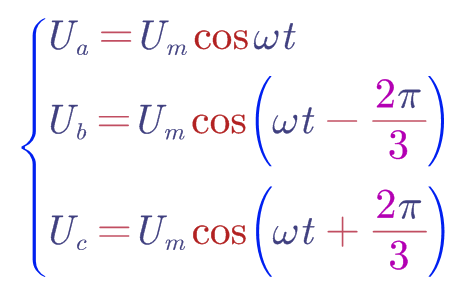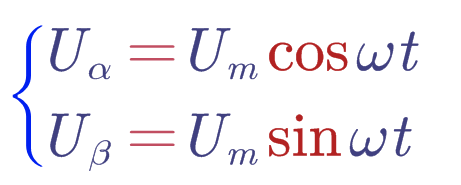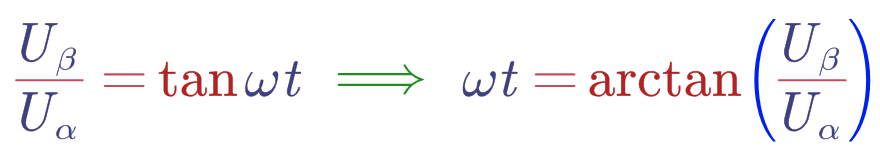FOC学习笔记(六)—–SVPWM扇区判断
一、理论分析
在反Park变换一节我们知道,经过反Park变换之后,我们得到Uα和Uβ如下,可能会有人有疑问,有Clark变换,Park变换,反Park变换,怎么就是没有反Clark变换呢?其实反Clark变换相当于集成到SVPWM里面了,接下来我们来分析:
Calrk变换是三相到两相的变换,Ia,Ib,Ic经过Clark变换之后得到Iα和Iβ,所以这里反Clark变换应该是两相到三相的变换,Uα和Uβ变换得到Ua,Ub,Uc。这里我们反过来看,因为我们知道电机正常转动时三相相电压的情况的,如下:
即为三相互差120度的对称三相正弦。我们把这个结果带入到Clark变换的式子中去,因为从后往前推导相当于还是进行Clark变换。
带入后经过合并计算:
其中Um是三相绕组的相电压幅值,至于大小为什么是sqrt(3)Udc/3,请移步这篇文章看相电压基波幅值。
到这里总之我们是得到了一个看起来很简单的结果
把结果单独提取出来如下:
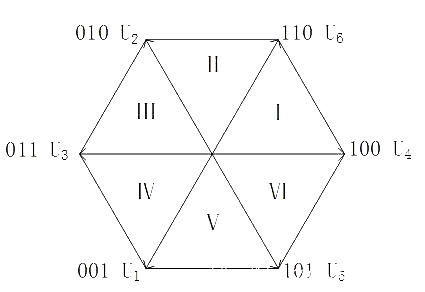
其中的Ωt就是θ,有了θ还不好判断扇区吗?那肯定很容易啦,扇区都是按照角度划分好的:
再推导一步就可以得到θ的公式:
这里就遇到一点小问题,可以看到要进行计算θ要进行反正切的运算,这对MCU来说是灾难,此运算的时间复杂度很高,MCU计算压力有点大,所以我们能不能找一个退而求其次的方法呢,通过人为的继续推导一步,来减少MCU的计算压力,是有的:
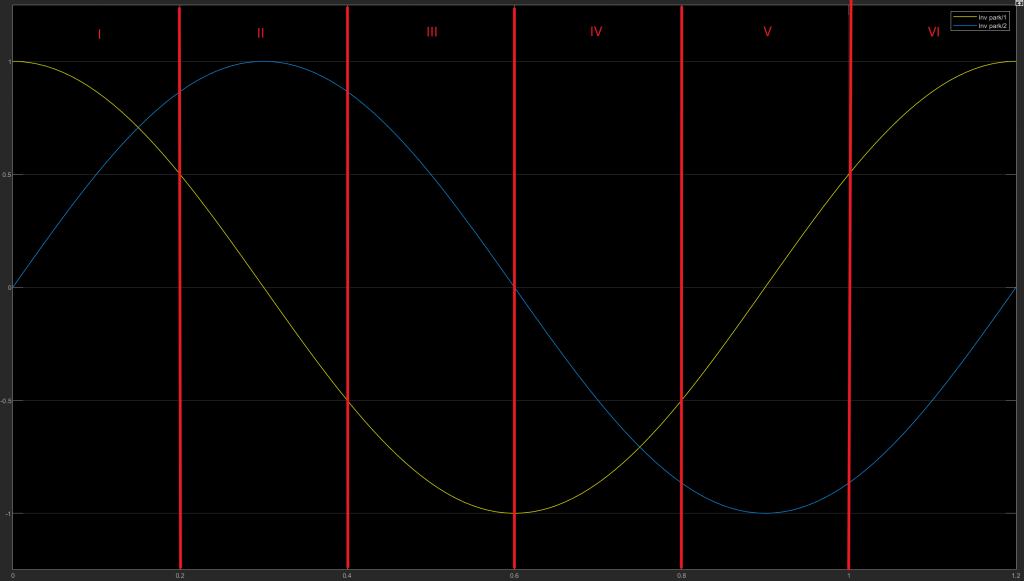
我们把Uα和Uβ的波形拉出来分析一下,黄色的是Uα,蓝色的是Uβ,我们均匀的按照角度划分为六个扇区:
有没有一种可能,我们只对Uα和Uβ进行定性分析,只看大于零还是小于零,而不进行反正切的运算就对扇区就行判断呢,完全是可以的。
接下来我们分析:
第一扇区:
从波形图可以看得出来,在第一扇区内,Uα和Uβ都大于0。另外,第一扇区的角度范围是0-60度,所以第一扇区的角度正切值tan(θ)的范围是:0<tan(θ)<sqrt(3)。即0<Uβ/Uα<sqrt(3),由于Uα>0,所以不等式两边同时乘以Uα,不等式不变号:即sqrt(3)Uα – Uβ > 0,两边都乘以1/2,不等式不变号,即:(sqrt(3)Uα – Uβ)/2 > 0。为什么要乘以1/2?因为这个值很特殊,在矢量作用时间的计算中也要用到它,所以我们这里保持一致,把这个变量保存下来,多次利用,避免重复运算。再计算一个特殊值:(-sqrt(3)Uα – Uβ)/2,因为Uα和Uβ均大于零,这里前面系数又都为负,所以这个多项式必然小于0。
所以结论是:在第一扇区:①Uβ > 0,②(sqrt(3)Uα – Uβ)/2 > 0,③(-sqrt(3)Uα – Uβ)/2 < 0。
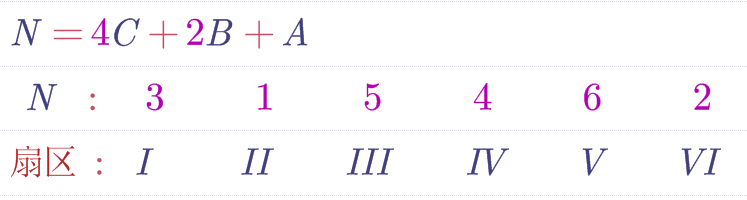
我们把①记作A,②记作B,③记作C,同理计算出其他五个扇区的A,B,C如下:
如图右边三列是最终的定性分析结果,可以看到每个扇区都不一样,所以我们只需要对A,B,C进行大于小于0的判断就可以确定扇区。
这里提供一个公式N = 4C + 2B + A,得到一个N值,其中A的值是:若A>0则A = 1,否则A = 0,B,C同理。可以发现这其实就是8421码的编码方式,只不过这里只有三位编码而已,我愿称之为421编码。计算出来一个N值之后,N值就和扇区号I~VI具有一一对应关系。这里直接给出结论,也可以自己计算。
至此实际上从理论上我们已经可以通过Uα和Uβ进行扇区判断了,接下来就通过Matlab仿真实现扇区判断:
二、Matlab仿真
创建一个SVPWM子模块,我这里是已经过了完整的SVPWM模块仿真,我们这里只看扇区判断部分就好,这里看到SVPWM模块会输出扇区号:
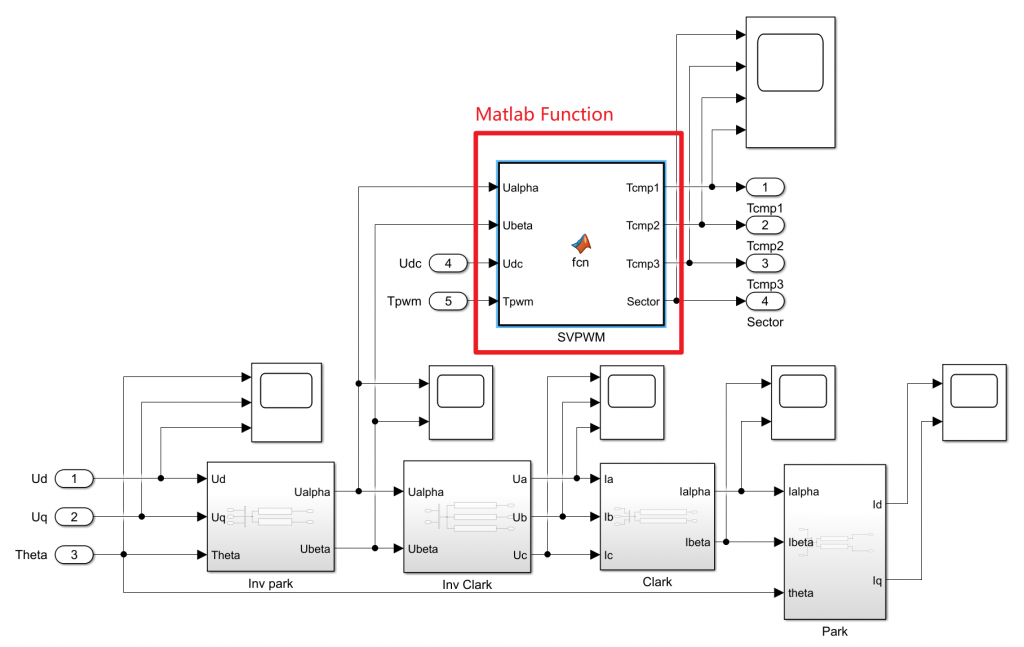
打开SVPWM模块看一下内部代码:
function[Tcmp1,Tcmp2,Tcmp3,Sector] = fcn(Ualpha,Ubeta,Udc,Tpwm)
%=============Initial========================
N = single(0);
Tcmp1 = single(0);
Tcmp2 = single(0);
Tcmp3 = single(0);
%=============A B C statement================
A = Ubeta;
B = (sqrt(3) * Ualpha - Ubeta)/2;
C = (-sqrt(3) * Ualpha - Ubeta)/2;
%============Sector Judgment=================
if(A > 0)
N = single(1);
end
if(B > 0)
N = N + single(2);
end
if(C > 0)
N = N + single(4);
end
switch(N)
case 1
Sector = 2;
case 2
Sector = 6;
case 3
Sector = 1;
case 4
Sector = 4;
case 5
Sector = 3;
otherwise
Sector = 5;
end
可以看到内部的计算实际上和我们的理论分析是完全一致的,进行ABC的计算然后进行扇区号的列表对应返回扇区号。
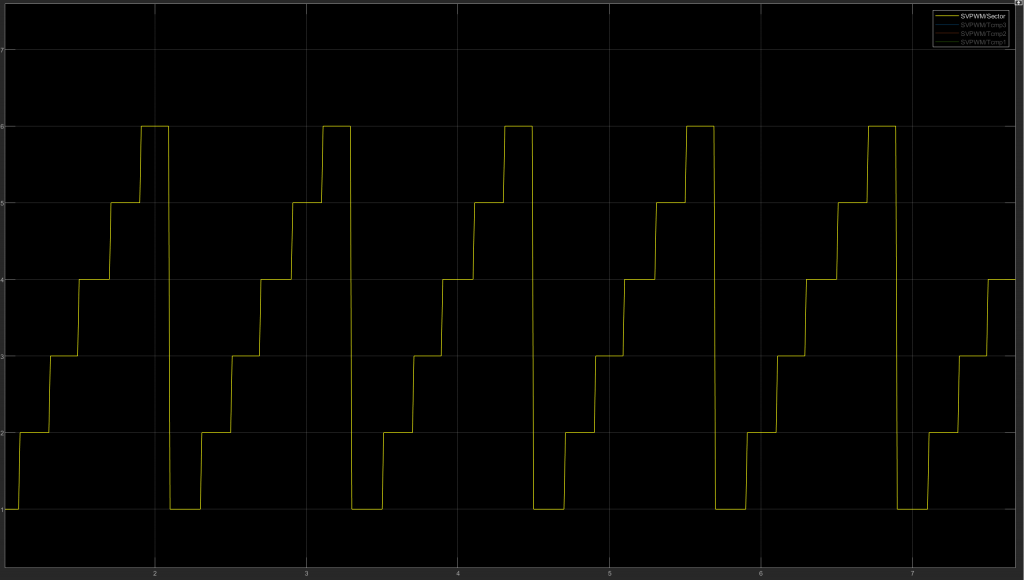
运行之后查看Sector输出,可以看到扇区号返回符合我们预期,1-6循环切换。
三、硬件平台实现
函数源码:
/*根据Ualpha和Ubeta判断当前扇区*/
SectorJudgement_t getSectorNumber(AlphaBetaCoord_t uAlphaBeta)
{
SectorJudgement_t SectorStructure_temp;
/*扇区判断数据N清零,防止随调用次数不断累加*/
SectorStructure_temp.mu8_SectorJudgement_N = 0;
/*计算扇区判断中间变量ABC*/
SectorStructure_temp.mf_SectorJudgement_A = uAlphaBeta.mf_Beta;
SectorStructure_temp.mf_SectorJudgement_B = (1.7320508 * uAlphaBeta.mf_Alpha - uAlphaBeta.mf_Beta);
SectorStructure_temp.mf_SectorJudgement_C = (-1.7320508 * uAlphaBeta.mf_Alpha - uAlphaBeta.mf_Beta);
/*由中间变量ABC根据公式N=A+2B+4C计算N值*/
if(SectorStructure_temp.mf_SectorJudgement_A > 0)
{
SectorStructure_temp.mu8_SectorJudgement_N += 1;
}
if(SectorStructure_temp.mf_SectorJudgement_B > 0)
{
SectorStructure_temp.mu8_SectorJudgement_N += 2;
}
if(SectorStructure_temp.mf_SectorJudgement_C > 0)
{
SectorStructure_temp.mu8_SectorJudgement_N += 4;
}
/*由N值通过查表法查出扇区号*/
if(SectorStructure_temp.mu8_SectorJudgement_N > 0 && SectorStructure_temp.mu8_SectorJudgement_N <= SECTOR_NUM)
SectorStructure_temp.me_Sector = e_SectorIndex[SectorStructure_temp.mu8_SectorJudgement_N];
/*N值不合法*/
else
SectorStructure_temp.me_Sector = SECTOR_ERROR;
return SectorStructure_temp;
}数据结构:
/*扇区号枚举*/
typedef enum
{
SECTOR_ERROR = 0,
SECTOR_1,
SECTOR_2,
SECTOR_3,
SECTOR_4,
SECTOR_5,
SECTOR_6
}SectorNum_e;
/*扇区判断相关结构体*/
typedef struct
{
float mf_SectorJudgement_A;
float mf_SectorJudgement_B;
float mf_SectorJudgement_C;
uint8_t mu8_SectorJudgement_N;
SectorNum_e me_Sector;
}SectorJudgement_t;
typedef struct
{
float mf_Alpha;
float mf_Beta;
}AlphaBetaCoord_t;运行查看输出:
输出结果完美和仿真一致,至此扇区判断部分完结!