FOC学习笔记(七)—–SVPWM之矢量幅值
有关幅值,包括三相相电压幅值,线电压幅值,六个非零基本矢量幅值,任意角度合成空间电压矢量幅值,SVPWM模块输出的相电压基波幅值等
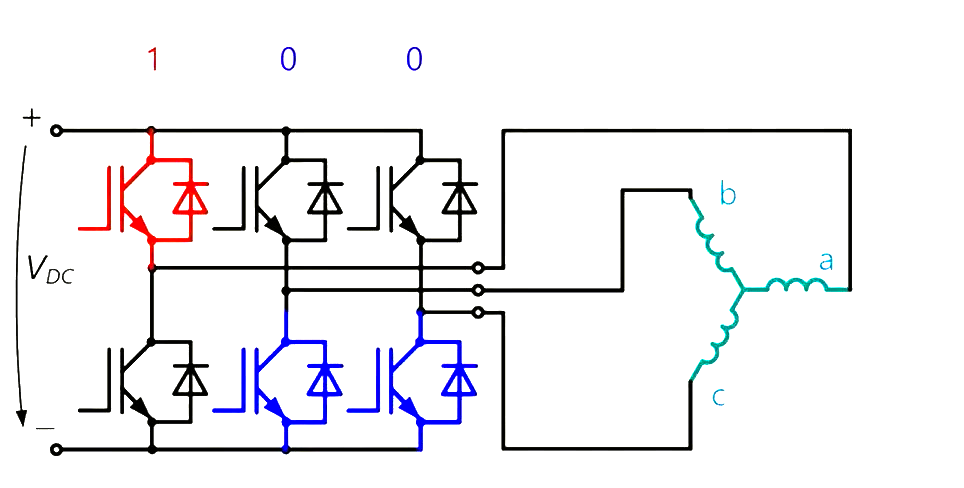
所有的幅值都要从母线电压开始说起,母线电压就是三相逆变器的直流侧供电电压,一般用Udc或Vdc表示,如下图最左侧的直流电压VDC就是母线电压。
1.相电压幅值:
说相电压就必须提到中性点,或者说N点,上图中就是abc三相绕组中间接在一起的那个点,所谓相电压就是三相绕组的对外端子到N点的电压,一般使用Uan,Ubn,Ucn表示,说白了就是每一相绕组两端的电压。
大家都知道,在SVPWM中三相逆变器的每一个全桥,同一时间只有上桥臂打开或者下桥臂打开,不能同时打开上下桥臂,不难看出如果同时打开上下桥臂,那意味着直流侧供电短路,BOOM!!
所以我们定义一个函数,S(x) (x=a或b或c),当上桥臂MOS闭合下桥臂MOS断开时S(x) = 1,相反当上桥臂MOS断开下桥臂MOS闭合时S(x) = 0,如此一来整个三相逆变器的六个MOS开关共有2³ = 8种开关状态,其中两中特殊状态。S(a) = S(b) = S(c) = 1,说人话就是三个上半桥臂MOS全部闭合,三个下半桥臂MOS全部断开,这种情况相当于三个定子绕组全部施加了Udc的电压,没有电压差所以定子绕组中没有电流流过。与此对应的还有一种情况:S(a) = S(b) = S(c) = 0,也就是全部下桥臂MOS闭合,上半桥臂MOS全部断开,这种情况更加简单,三相定子绕组全部接地了,直流电压根本没有过来,自然没有电流。除此之外还有六个正常的情况。
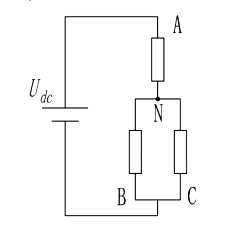
我们以上图这种情况(状态100)举例,第一个全桥上桥臂MOS闭合,电压通过第一个上桥臂MOS进入到a相绕组,然后分两路分别通过bc绕组,其余两个全桥下桥臂MOS闭合,经过第二和第三个全桥的下桥臂MOS,回流到地,等效电路如下图:
根据欧姆定律分压可以得到,A相绕组两端电压,也就是A相的相电压Uan = (2*Udc)/3。b相绕组和c相绕组并联故bc和c相的相电压相同Ubn = Ucn = (-Udc)/3。同理可以得到另外五种MOS管开关状态的相电压。
| S(a) | S(b) | S(c) | Uan | Ubn | Ucn |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 2Udc/3 | -Udc/3 | -Udc/3 |
| 0 | 1 | 0 | -Udc/3 | 2Udc/3 | -Udc/3 |
| 1 | 1 | 0 | Udc/3 | Udc/3 | -2Udc/3 |
| 0 | 0 | 1 | -Udc/3 | -Udc/3 | 2Udc/3 |
| 1 | 0 | 1 | Udc/3 | -2Udc/3 | Udc/3 |
| 0 | 1 | 1 | -2Udc/3 | Udc/3 | Udc/3 |
| 1 | 1 | 1 | 0 | 0 | 0 |
由上表可以看到,相电压最大可以达到2Udc/3,但是因为是直流供电,MOS只有开关两种状态,所以相电压只有0,Udc/3,2Udc/3,-Udc/3,-2Udc/3五种状态,而不是连续的正弦波。
2.线电压幅值
线电压就是三相绕组对外的三根线之间的电压,我们已经拿到了相电压,线电压的计算就比较简单了,Uab = Uan – Ubn,Uac = Uan – Ucn,Ubc = Ubn – Ucn。由上表列表如下:
| S(a) | S(b) | S(c) | Uab | Uac | Ubc |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | Udc | Udc | 0 |
| 0 | 1 | 0 | -Udc | 0 | Udc |
| 1 | 1 | 0 | 0 | Udc | Udc |
| 0 | 0 | 1 | 0 | -Udc | -Udc |
| 1 | 0 | 1 | Udc | 0 | -Udc |
| 0 | 1 | 1 | -Udc | -Udc | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
注意:等等,等等,相电压和线电压不满足sqrt(3)的关系了????这里提一下,相电压和线电压满足sqrt(3)的关系是有前置条件的,相电压都是正弦波的情况下才满足。我们这里三相的相电压都只是离散的五种状态组成的阶梯如下图,所以这里不满足sqrt(3)倍的关系
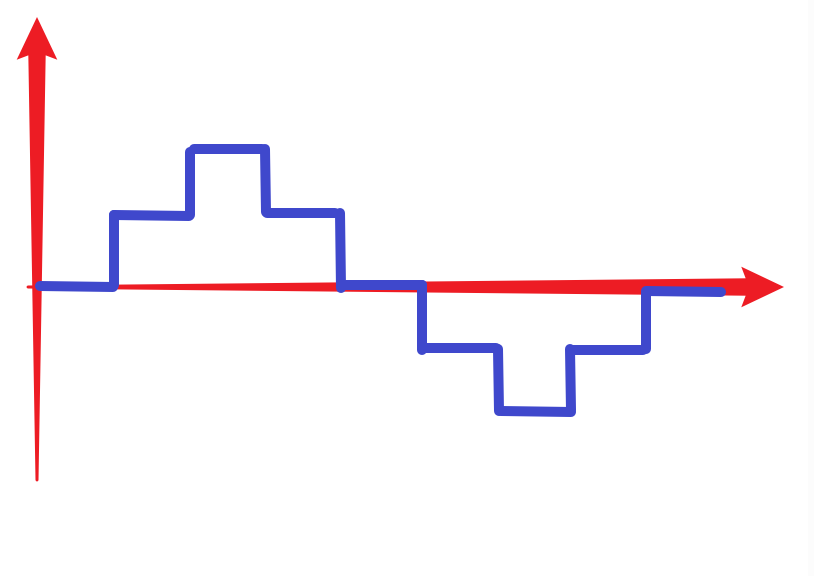
结论:线电压幅值为Udc。
3.六个非零矢量的幅值
我们仍然以其中一种MOS管开关状态为例,计算空间电压矢量的大小,三相绕组在空间上互差120度,这里依然以,MOS管开关状态100为例,此时A相绕组上相电压为2Udc/3,BC相绕组上相电压为-Udc/3。我们通过图示进行观察三相相电压合成空间矢量大小.
注意:电压本是标量,由于这里再空间上有互差120度的原因,赋予了他一个方向,所以在这里可以看作一个空间电压矢量。
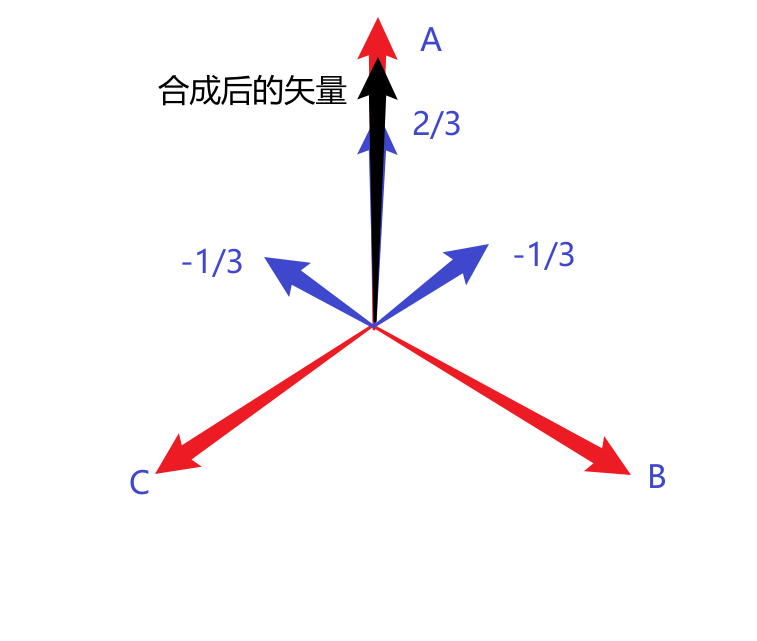
由上图可以看出,图中红色部分是三相坐标系互差120度,蓝色部分是三相绕组分别产生的空间电压矢量,黑色部分是三个部分进行矢量合成之后得到的合成电压矢量,大小为Udc,对,最终的合成矢量大小是Udc,但是要注意,到目前为止我们都还是在三相坐标系下进行分析和计算,所以这是在abc三相坐标系下的大小!!同理,其他五种MOS开关状态也可以使用同样的方法得到合成的空间电压矢量,如下图:
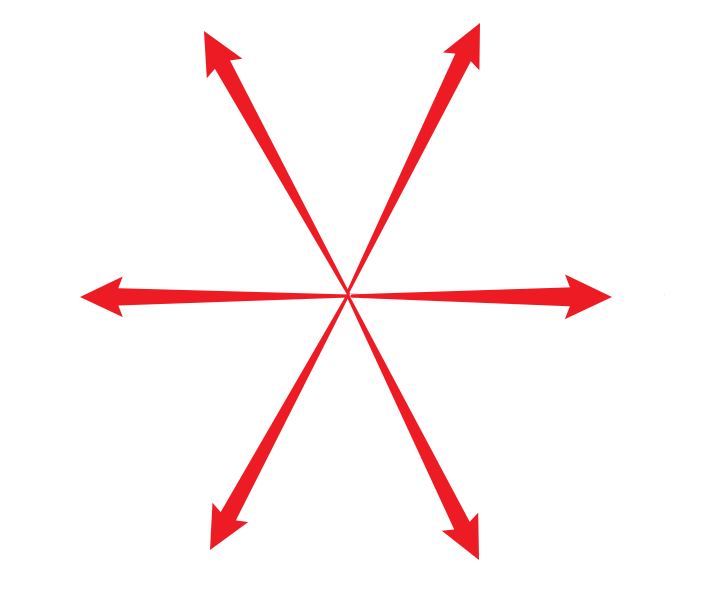
六个非零矢量大小为Udc,空间互差60°,注意,这六个矢量只是用于合成其他任意角度矢量的基向量(当然还有两个零矢量)。
不知道大家有没有发现两个问题。
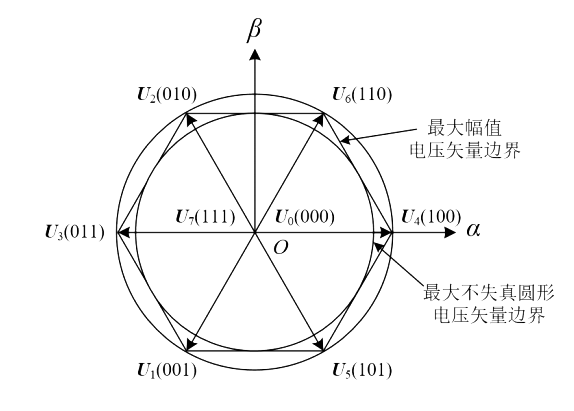
其一,我们要使用伏秒平衡原则,使用这八个矢量去合成任意角度的矢量,那么我们能合成一个角度与水平夹角30°,大小为Udc的矢量吗,如下图?
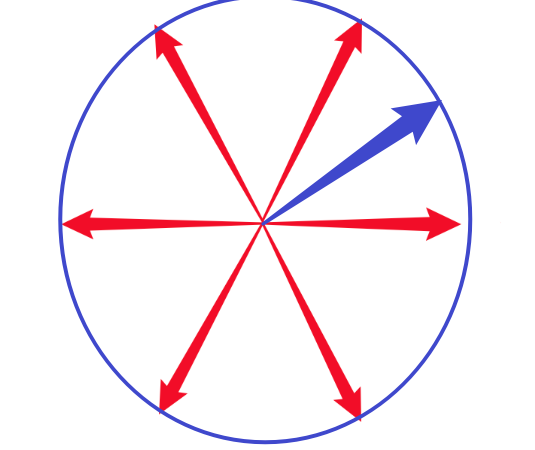
答案是不能。我们没办法合成一个半径为Udc的圆形矢量范围,我们只能合成一个六边形范围。说明:假如要合成30°的矢量,我们就需要使用0°和60°的两个基本矢量,使用相同的作用时间,那就意味着是两个大小是Udc/2且互差60°的矢量去合成,我们能得到多大的合成矢量呢,计算之后不难发现,只能得到sqrt(3)*Udc/2大小的合成矢量(也就是六个非零矢量的端点连起来组成的正六边形的边界)。所以我们没办法得到大小为Udc的圆形矢量范围。那么我们最大能得到多大的圆形的合成矢量范围呢,就是sqrt(3)*Udc/2,是上述正六边形的内切圆。如下图:
我们知道,当给三相空间上互差120°的三相定子绕组上通入时间相位上也互差120°的三相对称交流电流的时候,在定子绕组周围的空间会产生一个幅值是相电流幅值1.5倍的,角速度和通入的正弦交流的角速度相同的旋转矢量。反之亦然,我们定子绕组周围产生了一个旋转的矢量,那么三相绕组内的电流也必然是符合要求的对称三相电流。所以我们只需要花心思在合成一个圆形的电压矢量范围,电流就自然是三相对称正弦信号了。
其二,很多资料上都说,六个非零矢量的大小是2Udc/3,这是为什么呢?
其实大家细想一下可以发现,到目前为止,我们都是在三相坐标系下进行讨论和计算,但是我们使用基矢量进行合成任意矢量的时候实则是在正交坐标系下完成,这样更符合我们的直觉,因为我们早都习惯了正交分解合成那一套,我们高中做的力的正交分解等等就是。如果要在三相坐标系下进行合成,其实非常麻烦,矢量要往三个坐标轴上投影等,所以这里涉及到一步从三相坐标系到两相正交坐标系的转换,整个过程类似Clark变换,但是目标坐标系的名字不叫α-β坐标系了而已,我们暂且称为x-y坐标系,所以这里涉及到等幅值变换,不知道的可以看这篇文章。所以,我们说六个非零基本矢量的大小是2Udc/3,是没有问题的,在讨论向量大小的时候要明确是什么坐标系,大部份资料已经默认了是在两相坐标系下,所以说大小是2Udc/3。
所以在x-y两相坐标系下,我们做最大可以得到多大的圆形矢量范围呢,由“其一”中的这句话:所以我们没办法得到大小为Udc的圆形矢量范围。那么我们最大能得到多大的圆形的合成矢量范围呢,就是sqrt(3)*Udc/2,是上述正六边形的内切圆。可以看到基本矢量和可以合成的圆形矢量范围的半径存在一个sqrt(3)/2倍的关系,我们可不可以用x-y二相系下的基本矢量大小直接乘以sqrt(3)/2得到在x-y二相系下的圆形矢量范围的半径呢?当然可以,因为本来就是用基本矢量合成的,等比例缩小就可以了。所以在x-y坐标系下,我们这里能得到的组最大圆形矢量范围的半径,就是(2Udc/3)*(sqrt(3)/2)=(Udc/sqrt(3))。这也就是相电压基波幅值(虽然说由上文,相电压最大能达到2Udc/3,但它不是正弦波啊,他是一个阶梯波动,根据FFT我们知道任何周期性波形都可以等效成一系列的正弦波的加和,如果等效成正弦波基波和高次谐波的加和,那他的基波幅值只有(sqrt(3)Udc/3)。),在这个范围内,我们可以得到一个完整的圆形矢量范围,所以,在这个范围内,相电压是三相对称正弦波,超出这个范围就不是正弦波了。由于是相电压是三相对称正弦波,所以线电压和相电压之间也就满足sqrt(3)倍的关系了,也就可以得到线电压幅值 =(Udc/sqrt(3)*sqrt(3) = Udc。一不小心顺便得到了电压利用率=100%的结论(电压利用率=三相绕组线电压幅值/母线电压)。
在六个非零矢量这一节,我们顺便把相电压基波幅值,电压利用率,圆形矢量空间半径也一并讲清楚了


太棒了!