FOC学习笔记(八)—–SVPWM相邻矢量作用时长计算
在第六节中讲了扇区判断,在SVPWM中还有以一个至关重要的部分没有讲,就是相邻矢量作用时长的计算,有了这一步骤,我们才能将Uα和Uβ转换成三相电压输出(当然这里实际上是六路PWM输出,给到三相逆变器进行输出三相电压驱动电机转动),下面直接开始讲相邻矢量作用时长的计算。
在这篇文章FOC学习笔记(七)—–SVPWM之矢量幅值中我们讲到,根据三相逆变器的MOS开关状态,可以在空间中产生八种空间电压矢量,其中有两种零矢量和六个非零矢量。毫无疑问我们就是要使用这个八个矢量作为向量基底,通过伏秒平衡原则进行任意方向和大小的矢量合成。如下图:
举例第 I 扇区,我们想要在第一扇区合成一个矢量,根据题目就知道,是由相邻的两个基础矢量进行合成,也就是(100)和(110)。既然是根据伏秒平衡原则进行合成,自然就存在一个作用时间的问题,同一时刻只有一个向量可以产生作用,通过分时在两个矢量中间进行切换,以达到两个矢量同时做用的效果。那就很好理解,也就是说,我们假设一个PWM周期的时间是Ts,那么(100)和(110)甚至还有(000)(111)两个零矢量,就要共同瓜分这Ts的时间。那么这四个矢量的时间要怎么进行合理的分配呢?这就是这一节要讲清楚的问题
在这一节FOC学习笔记(六)—–SVPWM扇区判断我们得到了一个结论如下:
进一步得到:
这也就是扇区判断的实现逻辑了,Uα,Uβ作为整个SVPWM模块的输入,所以无论是扇区判断还是相邻矢量作用时长计算,我们都要拿Uα,Uβ来做文章,所有的信息都要从Uα,Uβ里面来得到。
这里我把第 I 扇区摘出来如下图:
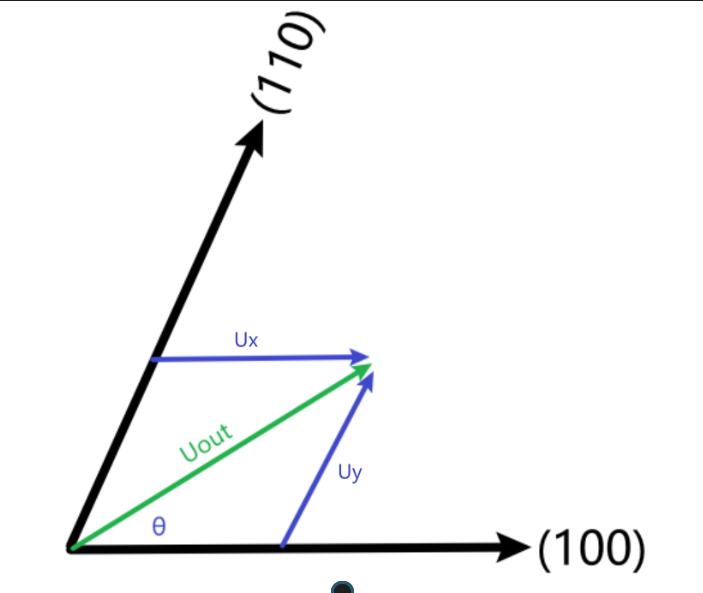
这里Ux和Uy就是合成矢量时两个基本矢量的等效大小,根据伏秒平衡原则我们可以列出表达式如下:
其中Tx为(100)矢量作用时间,Ty为(110)矢量作用时间,Ts为一个完整PWM周期的时间,这就是一个伏秒平衡原则的公式体现,至于为什么要乘以2Udc/3; 由FOC学习笔记(七)—–SVPWM之矢量幅值我们知道,六个非零矢量在两相坐标系下的大小是2Udc/3,所以乘以之后我们就得到两个基本矢量的大小了。
继续看上图,我们把Uout * Cos(θ)和Uout * Sin(θ)使用Ux和Uy表示出来:
到这里应该没有任何问题,纯纯的正交分解,细心一点你可能感受到了上面这个式子中什么cos(60°),sin(60°),这些纯纯是在两相正交坐标系下的操作了,虽然Ux和Uy夹角60°,我们也不是按照三相坐标系来操作的,纯正交坐标系下的操作,这也印证了FOC学习笔记(七)—–SVPWM之矢量幅值中讲的基本矢量的幅值为什么时2Udc/3,这步操作已经回到正交坐标系了。
我们把上面两组=个方程组连理带入一下:
懵了吧,脑瓜子嗡嗡的了吧,仔细看也不复杂,只是把Ux和Uy带入进去往前推导了一下。不知道你发现了没,到目前为止为什么还没有跟Uα和Uβ扯上关系啊,明明Uα和Uβ是整个SVPWM算法的唯一输入,不跟Uα和Uβ扯上关系那不纯白扯吗???我知道你很急但你先别急,就差一步啦,这是我们扇区判断时的结论:
这不就对上了吗Uout * Cos(θ)就是Uα;Uout * Sin(θ)就是Uβ!!!所以就有:
这不就妥了嘛,我们成功使用Uα,Uβ,Udc,Ts四个已知量表示了Tx和Ty(相邻矢量的作用时长)。
但是并没有结束,因为这只是第一个扇区的情况,其他的扇区也要照猫画虎推导一下。我这里继续给出第二扇区的计算过程,以此指出需要注意的点在哪里。
可以看到我圈出的(θ – 60)而不是第一扇区的θ了。这也不难解释,因为第二扇区范围内,θ的范围已经是(60,120)区间了,跨过去了整个第一扇区,所以正交分解计算的时候,自然要减去60°。其他扇区亦然。
这里我直接喂给你吃:
不难发现,不同扇区的Tx和Ty虽然略有不同,但基本上大部分还是存在共同的部分,我整理一下,六个扇区的Tx和Ty全部由三个部分组成只是正负号不同罢了,三个部分如下:
有意思了,这不就简单多了吗,这里还有一个小点不知道你有没有注意到,上式Y和Z中后面括号部分熟不熟悉??实际上我们在扇区判断一节里也遇到过这几个算子,后面代码处理的时候们就可以计算一次暂存起来重复使用,避免多次运算。下面通过列表把上面六个扇区的Tx和Ty结果列出来:
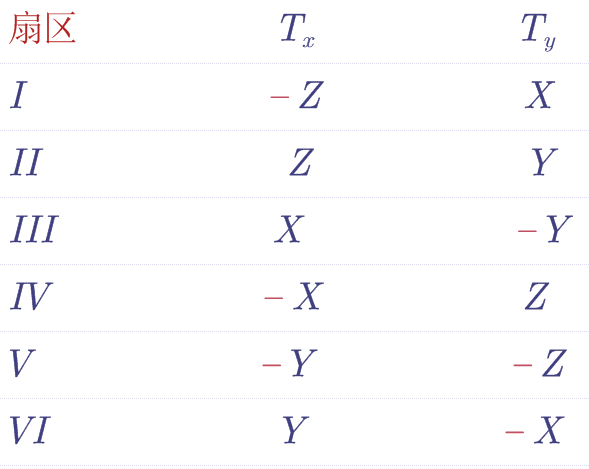
Tx和Ty只是非零矢量的作用时间罢了,别忘了每个PWM周期还有零矢量作用的时间哦,那么零矢量什么时候作用啊??一个PWM周期刚开始的时候?还是结束的时候?还是中间??实际上零矢量的作用是分成四段分布于每一个PWM周期内的,是不是觉得很麻烦,控制起来就很复杂,恐怖如斯,其实也还好,继续往下讲,一步一步来解决。
这里我们考虑一下实际MOS的开关,要知道MOS开关都是有寿命的,我们当然要尽可能少的开关,以延长寿命,怎么减少?我们不是伏秒平衡控制矢量合成吗,不是要一直切换作用的矢量吗, 不就是一直切换MOS的开关状态吗,有没有一种可能这样,我们每次切换作用的基本矢量的时候,只有一对MOS状态发生切换,举个例子:从(100)切换到(110),这其中就只有b相的MOS从上桥臂导通切换到了下桥臂导通,a和c相的MOS状态都没有发生变化。就是这个意思,实际上这是完全可能实现的,我们只需要合理安排基本矢量作用的顺序,并把两种零矢量(000)和(111)合理的插入到PWM周期里面,就可以了。
我这里还是以第一个扇区为例:
还是看这个图:
可以看到第一个扇区的相邻矢量是(100)和(110),还有两个零矢量(000)(111),这四个矢量如何有机的排布才能使得每次切换只有一个对桥臂的MOS发生切换呢?
(000)->(100)->(110)->(111)->(111)->(110)->(100)->(000)
这样不就妥了吗,可以看到(100)和(110)两个非零矢量在一个周期里面分别作用两次,零矢量一共作用四次。这里我把每一个扇区的切换顺序列出来
| 扇区 | 切换顺序 |
| I | (000)->(100)->(110)->(111)->(111)->(110)->(100)->(000) |
| II | (000)->(010)->(110)->(111)->(111)->(110)->(010)->(000) |
| III | (000)->(010)->(011)->(111)->(111)->(011)->(010)->(000) |
| IV | (000)->(001)->(011)->(111)->(111)->(011)->(001)->(000) |
| V | (000)->(001)->(101)->(111)->(111)->(101)->(001)->(000) |
| VI | (000)->(100)->(101)->(111)->(111)->(101)->(100)->(000) |
不难发现,所有的矢量切换顺序都是对称的,实际上我们使用STM32的定时器有一种中央对其的计数模式搭配PWM输出,就可以完美配合输出表格所列出的PWM波形,我们只需要管一侧的波形另一次定时器会自动帮我们完成。
老规矩,以第一个扇区为例,我根据上面表格第一行,把ABC三相驱动MOS的波形拆开绘制出来。
先看a相(第一位):
0->1->1->1->1->1->1->0
b相(第二位)
0->0->1->1->1->1->0->0
c相(第三位)
0->0->0->1->1->0->0->0
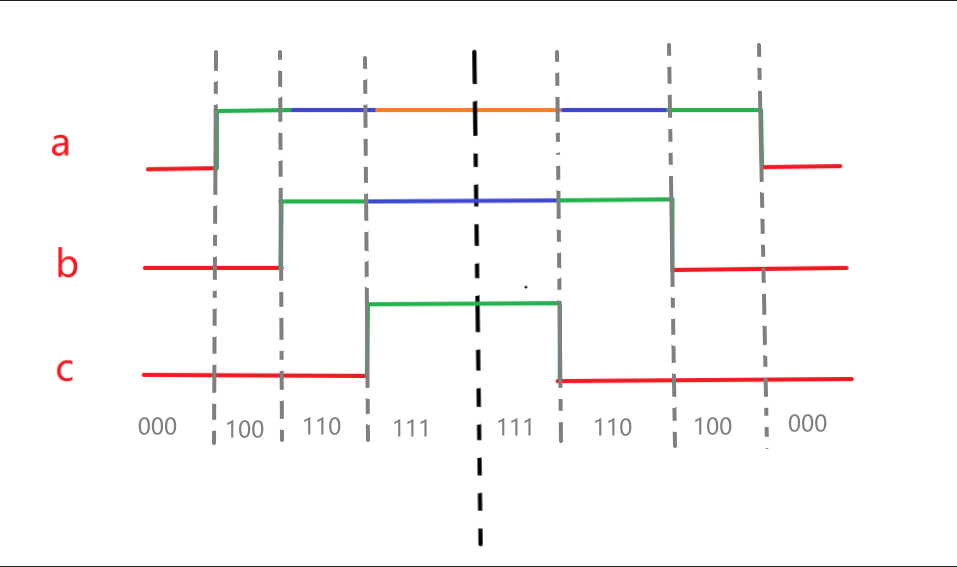
绘制成波形如下:
由于切换顺序是对称的,所以可以看出三相波形也是对称的,在使用STM32或者其他控制器的定时器的中心对齐模式的时候,我们只需要关心对称轴左侧的每一相发生从0->1的反转的时间就好了,对称轴右边定时器自己会搞定,所以我们来计算一下abc三相PWMf发生反转的时间Ta,Tb,Tc
首先明确一个PWM周期内有四个零矢量,两个(000),两个(111),这个上面也说到过,实在不行看一下上面那张表就看得出来,所以每一个零矢量的作用时间是(Ts-Tx-Ty)/ 4。
所以我们来看a相的波形图,发生反转的时间就是一个零矢量之后,所以此时Ta = (Ts-Tx-Ty)/ 4。
b相波形发生反转的时间是一个零矢量作用时间,加上一个(100)作用时间,(100)作用时间在第一扇区就是Tx,但是在一个PWM周期有两个(100)作用,所以一个(100)的作用时间就是Tx/2,所以b相发生反转的时间Tb = ((Ts-Tx-Ty)/ 4 )+ (Tx / 2) = Ta +(Tx / 2) 。
同理c相发生反转的时间Tc = Tb + (Ty / 2)。
同样道理以此类推其他所有扇区,实际上所有扇区内abc相MOS控制信号发生反转的时间都是以下几个部分的排列组合:
只需要根据扇区分配好这三个量就可以啦。至此我们就可以得到六个扇区的相邻矢量作用时间,其中的Ts实际上就是一个PWM周期定时器计了多少个值,例如:我的定时器溢出值是8400,中央对齐模式下,定时器从0往上计数到8400然后往下计数到0位一个PWM周期,所以我的Ts= 16800;这里计算出来的Ta,Tb,Tc,实际上就是PWM输出定时器的三个通道的比较值,可以直接更新到定时器比较寄存器里面去,就可以完成所需要的PWM输出。
我这里直接使用代码表示不同扇区的Ta,Tb,Tc的分配规律:
至此所有的相邻矢量作用时间计算完毕。


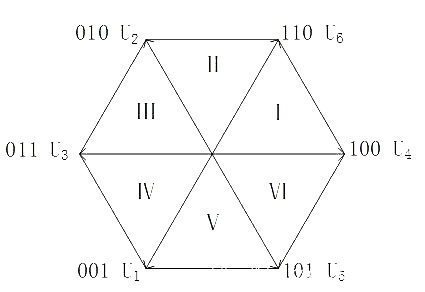
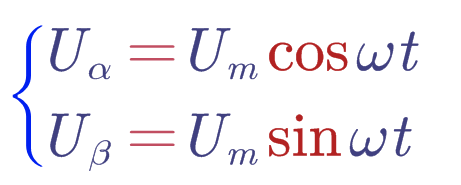
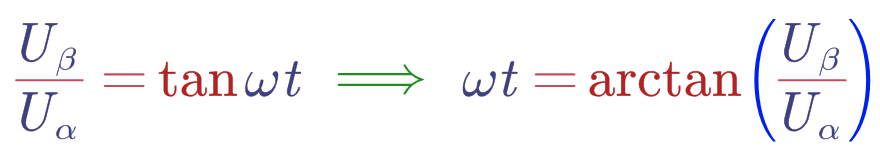
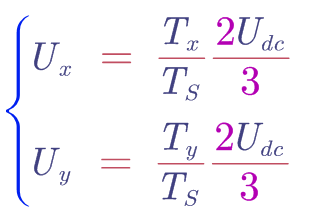
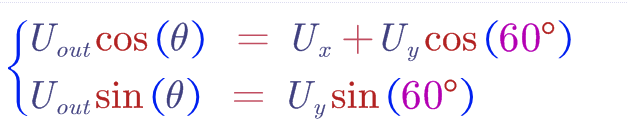



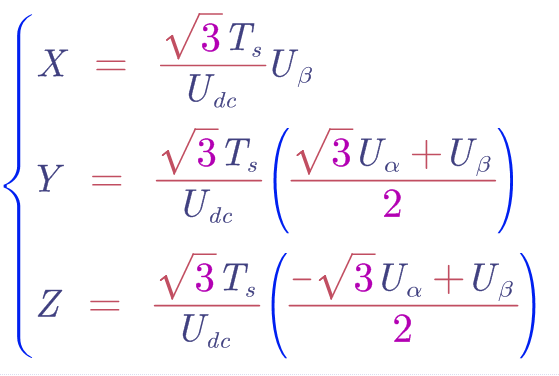
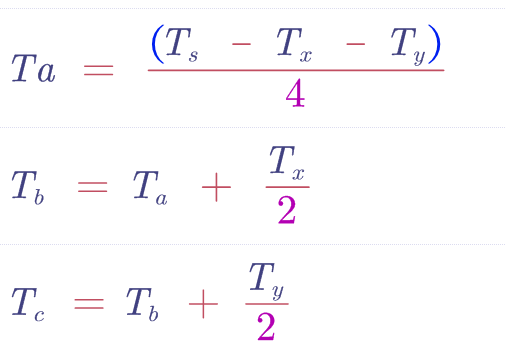

为什么扇区135和246推导公式中的Tx和Ty互换了呢?
相邻扇区切换的时候,因为有一个矢量是重叠的嘛,保持这个重叠的矢量不变,我大概是这样理解,可以说说你的想法讨论一下
请教博主orz,这个推导过程公式是用什么软件编辑的?
Axmath
请教博主,为了让定时器比较值和占空比的关系更直观,一般将PWM配置成模式1,这里计算出来的比较值实际是负的占空比值,那么在设置定时器比较值时是不是要相应改变一下呢?