FOC学习笔记(四)—-坐标变换之反Park变换
一、理论分析
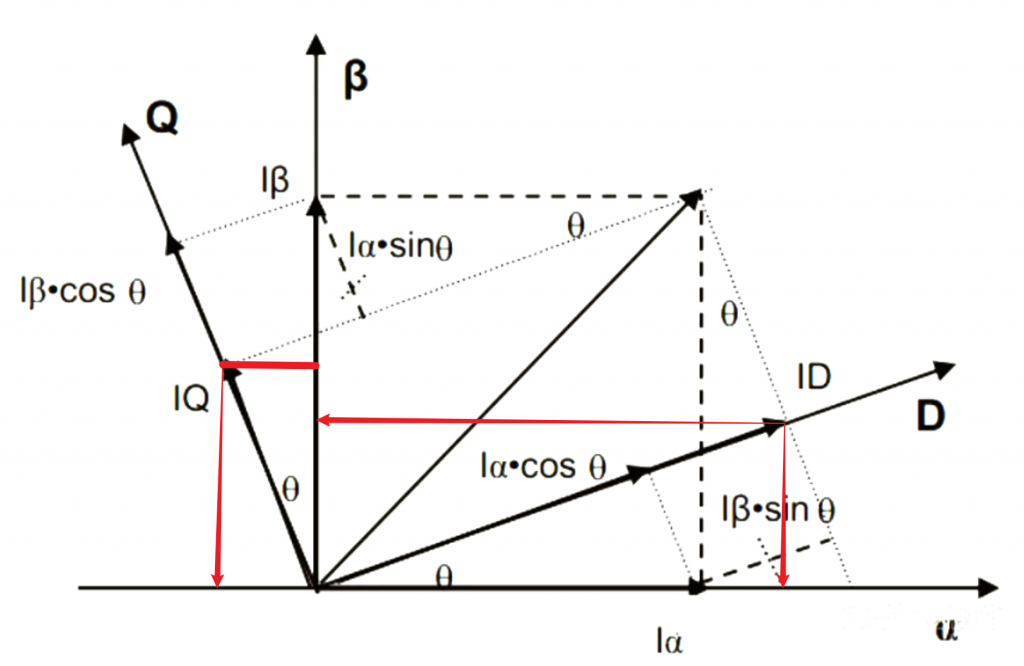
开局还是和Park变换一样的图,只不过这次正交分解的对象变了,这次变成把Ud和Uq往α-β坐标系上去分解,如下图所示:
不难看出,Ud在α坐标轴上的分量是Ud*cos(θ) ,Uq在α坐标轴上的分量是- Uq*sin(θ),Ud在β坐标轴上的分量是Ud*sin(θ) ,Uq在α坐标轴上的分量是Uq*cos(θ),所以经过反Park变换之后,我们可以得到如下结果;
注意:和Park变换不同的是,这里怎么变成Ud和Uq了呢,不是Id和Iq了,因为这里已经经过了PI控制器,计算之后已经是d-q坐标系下的电压了。
二、Matlab仿真
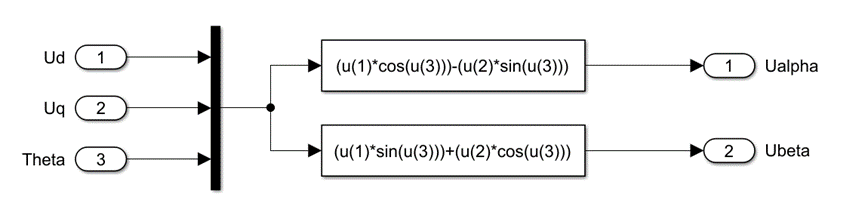
创建反Park变换子系统:
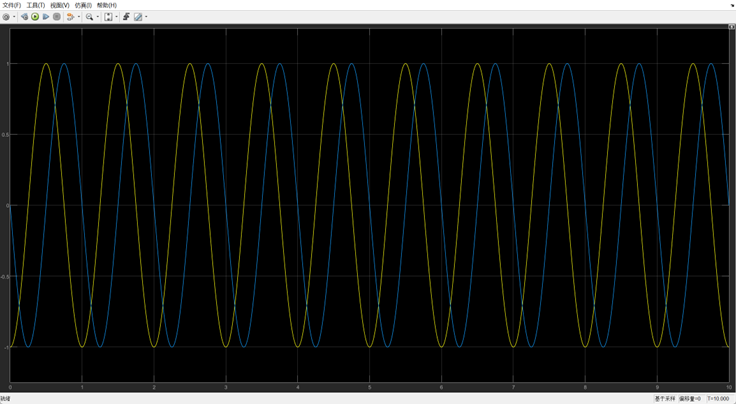
查看变换后波形:
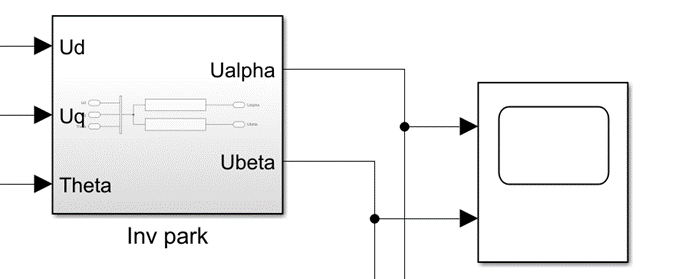
仿真结果:
三、MCU软件实现:

调用并打印结果
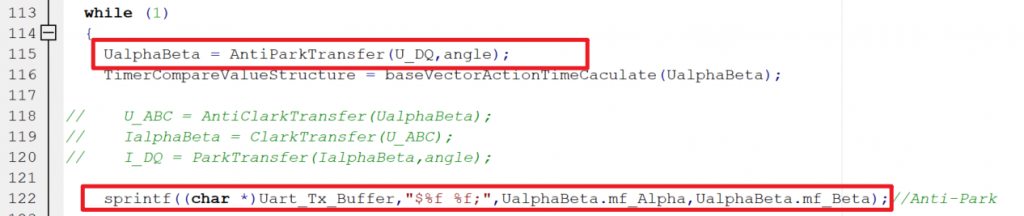
其中U_DQ模拟Ud = 0,Uq = 1;angle从0-360循环递增。查看输出结果:
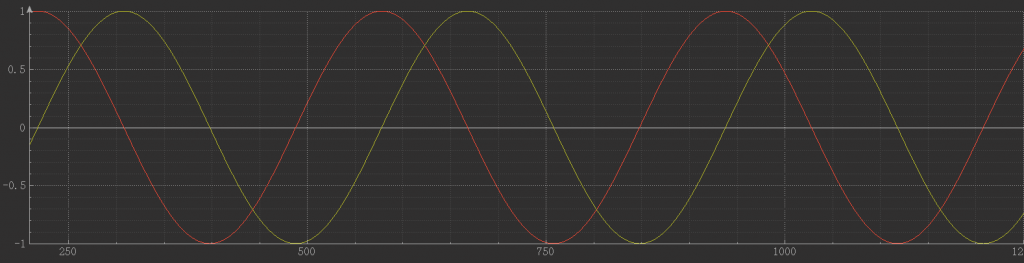
输出结果与Matlab仿真结果一致,反Park变换接口验证没有问题。


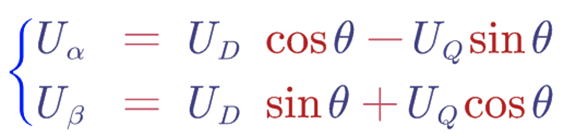
1 thought on “FOC学习笔记(四)—-坐标变换之反Park变换”